Theory
Aim
The aim is to create an interactive website that includes a simulation of the RRR Manipulator, pre- and post-quizzes, theoretical content on RRR Manipulator kinematics and applications, and a comparative analysis of KAN models with MLP.
Objective
Objective 1: Develop and compare the performance of Multilayer Perceptron (MLP), KAN: Kolmogorov-Arnold Networks(KAN), and Fourier-KAN, Fast-KAN, Kolmogorov-Arnold Networks (KAN) using Chebyshev polynomials for both forward and inverse kinematics of the RRR articulated robot.
Objective 2: Create an interactive MATLAB app to visualize the simulation of the RRR robot, allowing users to input joint angles and observe the corresponding end-effector positions in real-time.
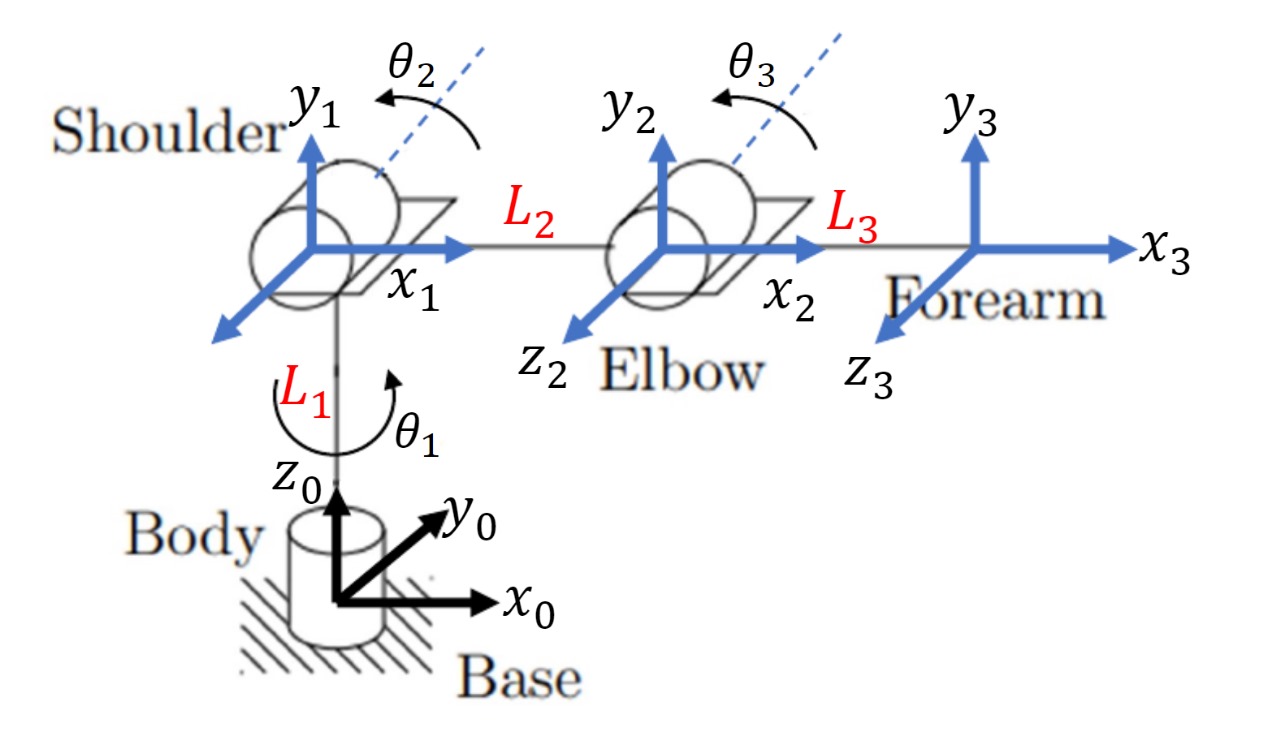
Introduction to the 3 DOF RRR Manipulator
In the field of robotics, manipulators are widely used to perform a variety of tasks ranging from simple pick-and-place operations to complex assembly processes. A 3 Degree of Freedom (DOF) Revolute-Revolute-Revolute (RRR) manipulator is a fundamental type of robotic arm that consists of three rotational joints. This configuration allows for a high degree of flexibility and a wide range of motion, making it suitable for many applications in industrial automation, medical robotics, and research.
Overview of Robotic Manipulators
Robotic manipulators are mechanical systems designed to interact with the environment through end-effectors, which can be tools, grippers, or sensors. The DOF in a manipulator refers to the number of independent movements it can perform. In the case of an RRR manipulator, each joint provides a rotational movement, leading to three distinct rotational motions.
The RRR Configuration
The RRR manipulator is named after its joint configuration:
- Revolute Joints: These joints allow rotational movement around an axis. In the RRR manipulator, all three joints are revolute, which means they provide rotation without any translational motion.
The typical structure of an RRR manipulator includes:
- Base Joint (J1): This is the first revolute joint, usually fixed to the base or ground, allowing the first link to rotate around a vertical or horizontal axis.
- Shoulder Joint (J2): The second revolute joint connects the first link to the second link, allowing rotation around a different axis.
- Elbow Joint (J3): The third revolute joint connects the second link to the third link or end-effector, providing the final degree of rotation.
Kinematics and Dynamics
Understanding the kinematics (motion) and dynamics (forces and torques) of the RRR manipulator is essential for its design and control:
- Forward Kinematics: This involves determining the position and orientation of the end-effector given the joint angles. It provides insight into how the manipulator reaches a desired point in space.
- Inverse Kinematics: This is the process of calculating the joint angles required to place the end-effector at a specific position and orientation. It is crucial for path planning and control.
- Dynamics: The study of forces and torques required to achieve the desired motion. This includes analyzing the effects of gravity, friction, and other external forces on the manipulator's movement.
Control Strategies
Effective control of a 3 DOF RRR manipulator involves several strategies:
- PID Control: Proportional-Integral-Derivative (PID) controllers are widely used for their simplicity and effectiveness in providing stable and responsive control.
- Model Predictive Control (MPC): This advanced method uses a model of the manipulator to predict future states and optimize control inputs.
- Adaptive Control: Adaptive strategies adjust control parameters in real-time to cope with changes in the manipulator's dynamics or external disturbances.
Forward Kinematics
The forward kinematics of the 3 DOF Manipulator is performed using DH Parameters which are considered to be standard for robot kinematics.
Table-1: DH parameters of the 3 DOF Manipulator
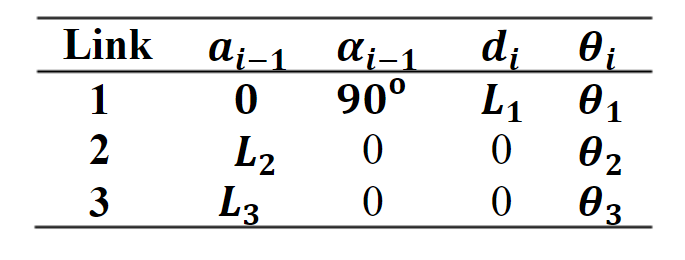
The position and orientation of the robot end-effector can be represented by the Homogeneous Transformation matrix.
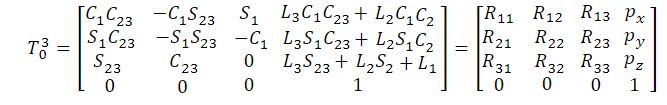
Where the px, py, pz represent the robot end-effector in x, y, z directions and R11…R33 represents the orientation of the robot end-effector.
Inverse Kinematics
In the Inverse Kinematics, the joint variables θ1, θ2, θ3 are determined using the geometrical approach. This approach solves the joint variable θi by projecting the robot onto the plane of xi-1 - yi-1 and then solving it with trigonometry.
The joint variables are given by the following equation:
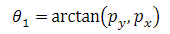
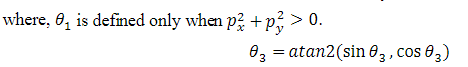

Importance and Applications
The 3 DOF RRR manipulator is crucial in various applications due to its simplicity and effectiveness:
- Industrial Automation: In manufacturing, RRR manipulators are used for tasks such as welding, painting, and material handling due to their precise control and flexibility.
- Medical Robotics: These manipulators can be employed in minimally invasive surgeries, where precise and controlled movements are essential.
- Research and Development: In academia and research institutions, RRR manipulators serve as testbeds for developing new algorithms in control systems, kinematics, and dynamics.


Conclusion
The 3 DOF RRR manipulator is a versatile and essential tool in the field of robotics. Its simple yet effective design allows for a wide range of applications, from industrial automation to advanced research. Understanding its kinematics, dynamics, and control strategies is crucial for developing efficient and precise robotic systems. As technology advances, the role of RRR manipulators will continue to expand, driving innovation and efficiency in various domains.


